VETORES
Vetores são entes geométricos que nos permitem estudar a orientação de objetos e funções. Um vetor pode ser simbolizado por uma letra com uma seta em cima, como por exemplo, 
(lê-se vetor v).
Graficamente, um vetor é representado por uma reta orientada e tem direção, sentido e valor numérico. Veja o quadro abaixo:
Vetor |
Direção |
Sentido |
Módulo ou valor numérico |
 |
horizontal | da esquerda para a direita | 10 unidades (10u) |
 |
horizontal | da direita para a esquerda | 6 unidades (6u) |
 |
vertical | de baixo para cima | 8 unidades (8u) |
 |
vertical | de cima para baixo | 4 unidades (4u) |
CÁLCULO VETORIAL
Adição Algébrica de Vetores
1. Vetores de mesma direção e sentido: adiciona-se e conserva-se a direção e o sentido.
Exemplo:
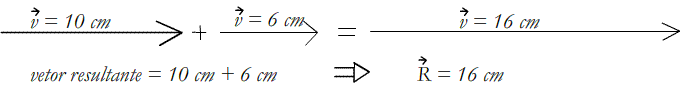
2. Vetores de mesma direção e sentidos opostos: subtrai-se o menor vetor do maior vetor. Fica a mesma direção e o sentido do maior vetor.
Exemplo:
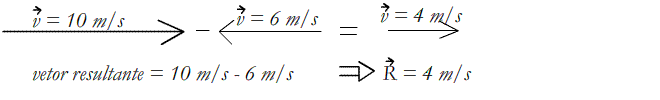
3. Vetores que formam ângulos entre si: aplica-se a regra do paralelogramo, que consiste em manter a direção e o sentido dos dois vetores, mas de forma que o ponto de início dos dois vetores fiquem unidos no mesmo ponto. Então, usa-se a lei dos cossenos para calcular o vetor soma resultante. Veja abaixo, dois vetores 
e 
. O cálculo é feito pela fórmula: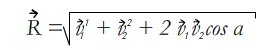 
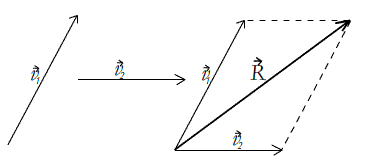
Exemplos:
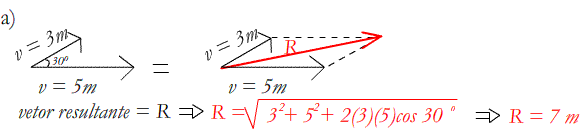
b) Casos particulares:
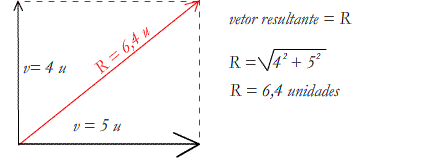
Quando ângulo igual a 90º, a regra acima se reduz ao Teorema de Pitágoras, porque cos 90º é igual a zero (0)
Quando ângulo igual a zero (0), a regra acima se reduz a adição de vetores de mesma direção e sentido.
Quando ângulo igual a 180º, a regra acima se reduz a adição de vetores de mesma direção e sentidos opostos.
Veja uma animação de adição com vetores em http://phet.colorado.edu/sims/vector-addition/vector-addition_pt_BR.html
NOTA: Para adicionar dois ou mais vetores também pode ser aplicado a Regra do Polígono.